haka
Mächtiger Krieger
- Mitglied seit
- 23.01.2005
- Beiträge
- 99
Ich habe keinen Plan wie man die Aufgabe lösen kann
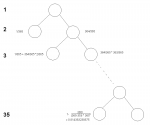
sie soll mit einem Baumdiagramm dargestellt werden
wir sollen außerdem das ganze für 365 tage berechnen also schaltjahre außer betracht lassen
vielleicht hat einer von euch ja eine idee
Aufgabe: Sie kommen in eine Gruppe von 35 Personen, die sich über unglaubliche Zufälle unterhalten. Um alle zu verblüffen, wetten Sie, dass mind. 2 der 35 am selben Tag wie sie Geburtstag haben. Welches Risiko gehen Sie mit dieser Wette ein?
vielen dank im voraus
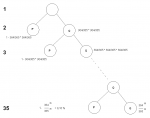
sie soll mit einem Baumdiagramm dargestellt werden
wir sollen außerdem das ganze für 365 tage berechnen also schaltjahre außer betracht lassen
vielleicht hat einer von euch ja eine idee
Aufgabe: Sie kommen in eine Gruppe von 35 Personen, die sich über unglaubliche Zufälle unterhalten. Um alle zu verblüffen, wetten Sie, dass mind. 2 der 35 am selben Tag wie sie Geburtstag haben. Welches Risiko gehen Sie mit dieser Wette ein?
vielen dank im voraus